3.1 Muestreo aleatorio.
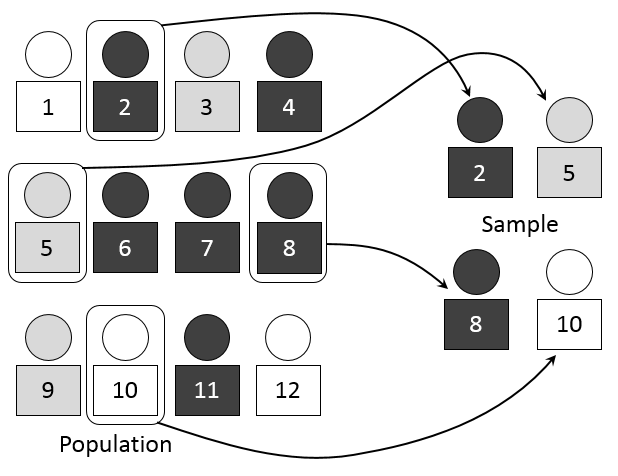Es la extracción de una
muestra de una población finita, en el que el proceso de extracción es tal que
garantiza a cada uno de los elementos de la población la misma oportunidad de
ser incluidos en dicha muestra. Esta condición garantiza la representatividad
de la muestra porque si en la población un determinado porcentaje de individuos
presenta la característica A, la extracción aleatoria garantiza matemáticamente
que por término medio se obtendrá el mismo porcentaje de datos muéstrales con
esa característica.
El muestreo aleatorio puede
ser de dos tipos:
ü Sin reposición de los elementos: Los
elementos extraídos se descartan para la siguiente extracción. Por ejemplo, si
se extrae una muestra de bombillas para inferir su vida media, no es posible la
reposición.
ü Con reposición de los elementos (Muestreo Aleatorio
Simple): Las observaciones se realizan con reemplazamiento de los
individuos, de forma que la población es idéntica en todas las extracciones y,
por tanto, cada observación es independiente de la anterior. En poblaciones muy
grandes, la probabilidad de repetir una extracción es tan pequeña que el
muestreo puede considerarse con reposición aunque, realmente, no lo sea.
Para realizar este tipo de
muestreo, y en determinadas situaciones, es muy útil la extracción de números
aleatorios mediante ordenadores, calculadoras o tablas construidas al efecto.
3.2 Muestreo al azar.
El
concepto básico de todo muestreo es el de la muestra al azar. Una muestra de
objetos de una población se llama al azar cuando todos los miembros de la
población tienen igual oportunidad de aparecer en la muestra. Es muy importante
insistir en que esto es igualmente válido para todos los miembros de la
población, tanto para los raros como para los típicos.
EJEMPLO.
El
plegonero desembarcado por un solo barco en Lowestoft suele tener (aquí
supondremos que siempre) una composición de longitudes suavemente uni-modal,
con la moda normalmente entre 28 y 30 cm, pero alguna vez, por ejemplo, una
entre 30, llega a ser hasta de 35 cm. Por lo tanto, si tomamos una muestra al
azar de plegonero de cada barco, una vez de cada 30, por término medio, tendrá
una moda de 35 cm o más, aunque normalmente estará entre 28 y 30 cm. Si
entonces un biólogo pesquero, apoyándose en una sola muestra, obtiene una moda
de 35 cm, esta desviación de la media de 29 cm no significará necesariamente
una muestra que no sea al azar, puesto que se puede dar este caso una vez de
cada 30; pero se puede comprobar tomando más muestras, por ejemplo tres
muestras, que sólo tendrán juntas una moda superior a 35 cm una vez entre
27.000.
3.3 Muestreo simple, doble, múltiple.
MUESTREO SIMPLE:
El procedimiento
empleado es el siguiente:
1) se asigna un
número a cada individuo de la población y;
2) a través de
algún medio mecánico (bolas dentro de una bolsa, tablas de números aleatorios,
números aleatorios generadas con una calculadora u ordenador, etc.) se eligen
tantos sujetos como sea necesario para completar el tamaño de muestra
requerido.
MUESTREO DOBLE:
Bajo este tipo de
muestreo, cuando el resultado del estudio de la primera muestra no es decisivo,
una segunda muestra es extraída de la misma población. Las dos muestras son
combinadas para analizar los resultados. Este método permite a una persona principiar
con una muestra relativamente pequeña para ahorrar costos y
tiempo. Si la primera muestra arroja un resultado definitivo, la segunda
muestra puede no necesitarse.
EJEMPLO
Al probar la calidad
de un lote de productos manufacturados, si la primera muestra arroja una
calidad muy alta, el lote es aceptado; si arroja una calidad muy pobre, el lote
es rechazado. Solamente si la primera muestra arroja una calidad intermedia,
será requerida la segunda muestra.
MUESTREO MÚLTIPLE
El procedimiento bajo
este método es similar al expuesto en el muestreo doble, excepto que el número
de muestras sucesivas requerido para llegar a unadecisión es más de dos muestras. Métodos de muestreo clasificados de acuerdo con las maneras usadas en seleccionar los elementos de una muestra pueden ser seleccionados de dos maneras diferentes:
a) Basado en el
juicio de una persona
b) Selección
aleatoria
3.4 Muestreo de aceptación, por lote, AQL, niveles de inspección,
manejo de tablas MIL-STD (militar standar).
MUESTREO
DE ACEPTACIÓN:
Un muestreo de aceptación
consiste en evaluar un colectivo homogéneo a través de una muestra aleatoria,
para decidir la aceptación o el rechazo del colectivo. Por tanto es necesario
tener presente en todo momento que, en un muestreo, lo que se está evaluando es
toda la población y no sólo la muestra, por lo que la cuestión es si una
población, con las características inferidas a partir de los datos de la
muestra observada, es aceptable o no.
La primera cuestión que se
plantea ante una inspección de recepción es si se realiza un muestreo o si es
precisa una inspección al 100%. Deming demuestra que la situación óptima
(mínimo coste esperado) es:
Ø Si p
< k1 / k2 Aceptar sin inspección.
Ø Si p
> k2 / k2 Realizar inspección 100%.donde:
Ø p:
Peor fracción defectuosa esperada del lote.
Ø k1:
Coste de inspeccionar una pieza.
Ø k2:
Coste de aceptar una pieza defectuosa.
De acuerdo con este criterio,
el muestreo no tiene sentido. No obstante hay que tener en cuenta lo siguiente:
v La
inspección por medios destructivos no puede ser 100% por razones obvias.
v En el
caso de lotes muy grandes la inspección 100% deja de ser 100% fiable debido a
factores como la fatiga, etc. Además en lotes grandes la relación entre el
tamaño de la muestra requerida y el tamaño del lote decrece, por lo que el
empleo de métodos de muestreo puede estar justificado.
POR
LOTE
La formación de un lote puede
influir en la eficacia del plan de muestreo de aceptación. A
continuación se enuncia tres recomendaciones para formar los lotes, aunque una
de ellas se debe ver como reserva. Los lotes deben ser homogéneos. Es decir,
las unidades que forman un lote en particular deben haber sido fabricadas bajo condiciones similares en cuanto a máquinas,
operadores, materia prima, tiempo (fechas), etcétera.
Cuando el lote se forma mezclando unidades de diferentes fuentes, el
muestreo de aceptación no es tan efectivo como se debe. Además la existencia de
lotes no homogéneos hace más difícil tomar acciones correctivas que
eliminan la causa de los productos defectuosos. De esa manera, cuando
se forme un pedido o embarque es mejor inspeccionar cada lote individual y
evitar aplicar la inspección a todo el pedido después de que se han mezclado
lotes. Los lotes deben ser formados de manera que no compliquen el manejo
de materiales del proveedor y del cliente. Todos los artículos de los
lotes deben ser empaquetados y embarcados con un mínimo de riesgo y
de forma que la selección de unidades de la muestra sea relativamente
fácil.
AQL
Se define como el porcentaje
máximo de unidades que no cumplen con la calidad especificada, que para
propósitos de inspección por muestreo se puede considerar como satisfactorio o
aceptable como un promedio para el proceso. El NCA también se lo conoce como
nivel de calidad del productor y se expresa en porcentajes de unidades que no
cumplen con la calidad especificada. Al ser el NCA el nivel de calidad que se
considera satisfactorio, entonces la probabilidad de aceptar un lote que tenga
esa calidad debe ser alta (0.95) A la probabilidad de aceptar lotes que tengan
un nivel da calidad aceptable (NCA), se lo designa con 1 – a, donde a es por lo
general un número pequeño (0.05, 0.10). Nótese que la probabilidad de aceptar
lotes de calidad aceptable no es igual a 1 y por tanto hay un riesgo de no
aceptar este tipo de lotes. A este riesgo que tiene probabilidad igual se le
conoce como riesgo del productor.
MANEJO DE TABLAS MIL- STD:
Determina el nivel de
inspección el cual está relacionado con el tamaño muestral. Usualmente se
utiliza el nivel II pero el nivel III se usa cuando el costo es alto. Los
planes especiales se utilizan con ensayos y son destructivos, en los cuales se
deseen tamaños mínimos.
3.5 Muestreo estratificado.
Muestreo estratificado Para
utilizar el muestreo estratificado, dividimos la población en grupos
relativamente homogéneos, llamados estratos. Después utilizamos uno de los dos
planteamientos: o bien seleccionamos aleatoriamente, en cada estrato, un número
específico de elementos correspondiente a la proporción del mismo en relación
con la población completa, o extraemos el mismo número de elementos de cada
estrato y después ponderamos los resultados considerando la proporción que el
estrato representa con respecto a la población total. Con cualquiera de los
planteamientos, el muestreo estratificado garantiza que cada elemento de la
población tenga posibilidad de ser seleccionado. El muestreo estratificado
resulta apropiado cuando la población ya está dividida en grupos de diferentes
tamaños y deseamos tomar en cuenta esta condición.
v Consiste en la
división previa de la población de estudio en grupos o clases que se suponen
homogéneos respecto a característica a estudiar y que no se solapen.
v Según la cantidad de
elementos de la muestra que se han de elegir de cada uno de los estratos,
existen dos técnicas de muestreo estratificado:
Ø Asignación
proporcional: el tamaño de cada estrato en la muestra es proporcional a su
tamaño en la población.
Ø Asignación óptima: la
muestra recogerá más individuos de aquellos estratos que tengan más
variabilidad. Para ello es necesario un conocimiento previo de la población.
EJEMPLO
Supongamos que los pacientes
de un médico están divididos en cuatro grupos de acuerdo con su edad. El médico
desea averiguar cuántas horas duermen sus pacientes. Para obtener una
estimación de esta característica de la población, podría tomar una muestra
aleatoria de cada uno de los cuatro grupos de edades y ponderar las muestras de
acuerdo con el porcentaje de pacientes en ese grupo. Éste sería un ejemplo de
una muestra estratificada. La ventaja de las muestras estratificadas es que,
cuando se diseñan adecuadamente, reflejan de manera más precisa las
características de la población de la cual fueron elegidas, en comparación con
otro tipo de muestras
integrantes
BERNABE GARCIA MELINA
MOLINA GREGORIO RIGOBERTO
ROSALES CARBAJAL ZULEYDI LIZET
SANTOS SANTOS JONATHAN GUSTAVO
